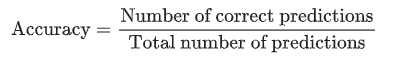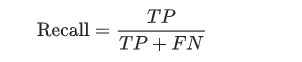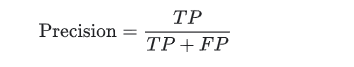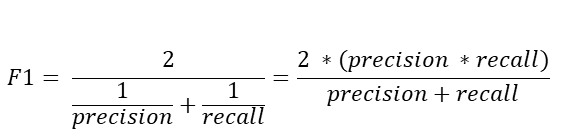How to Evaluate Your Machine Learning Models with Python Code!

You’ve finally built your machine learning model to predict future prices of Bitcoin so that you can finally become a multi-billionaire. But how do you know that the model you created is any good?

In this article, I’m going to talk about several ways you can evaluate your machine learning model with code provided! There are two parts to this article:

A) Evaluating Regression Models
B) Evaluating Classification Models

If you don’t know the difference between regression and classification models, check out here.

More specifically, I’m going to cover the following metrics:

R-Squared
Adjusted R-Squared
Mean Absolute Error
Mean Squared Error
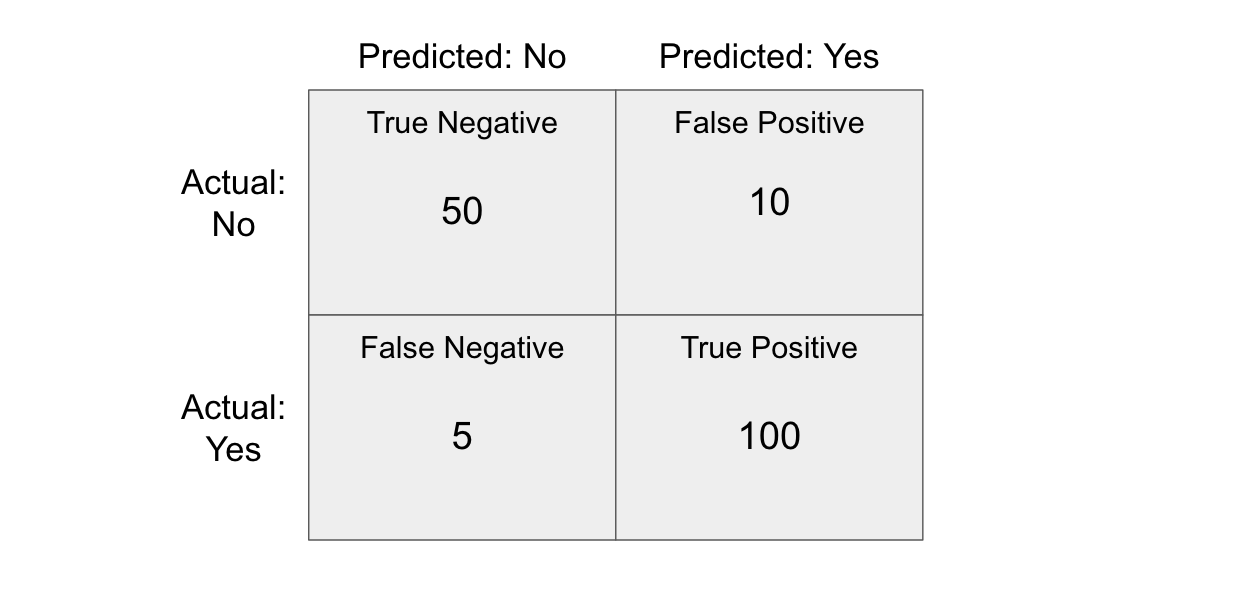
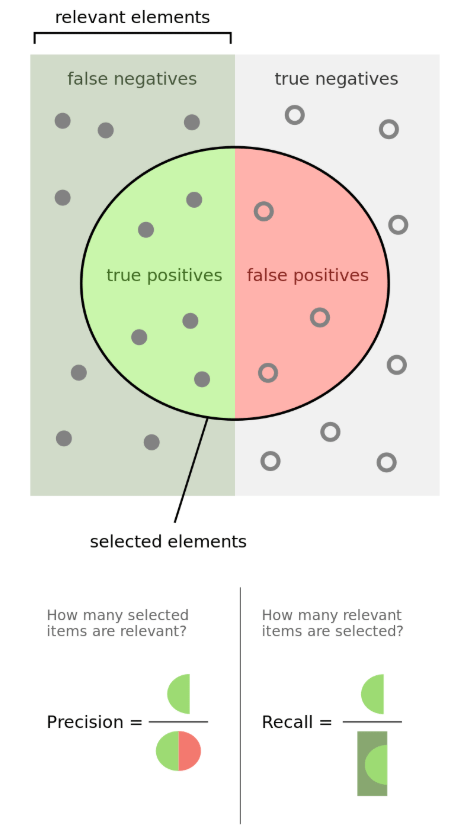
Confusion Matrix and related metrics
F1 Score
AUC-ROC Curve

A) Evaluating Regression Models

1. R-Squared

R Square is a measurement that tells you to what extent the proportion of variance in the dependent variable is explained by the variance in the independent variables. In simpler terms, while the coefficients estimate trends, R-squared represents the scatter around the line of best fit.

For example, if the R² is 0.80, then 80% of the variation can be explained by the model’s inputs.

If the R² is 1.0 or 100%, that means that all movements of the dependent variable can be entirely explained by the movements of the independent variables.

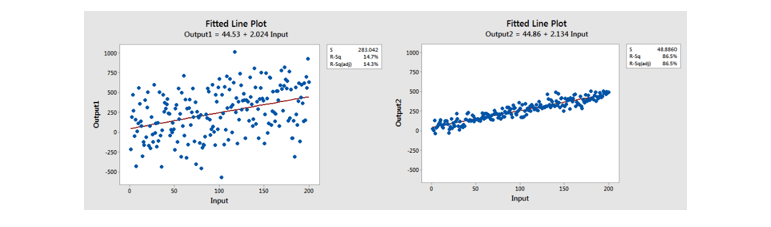
To show a visual example, despite having the same line of best fit, the R² on the right is much higher than the one on the left.

Comparison of a model with a low R² vs a high R²

The equation for R² is as follows:

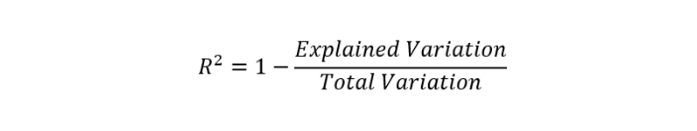
The Explained Variation is equal to the sum of squared residuals while the total variation is equal to the total sum of squared.

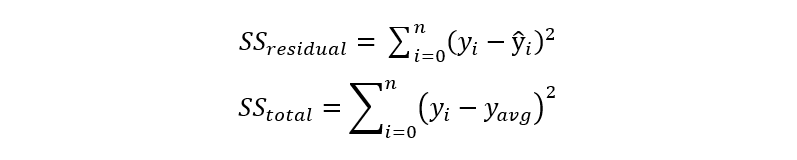
Now that you understand what R² is, the code is very straightforward!

from sklearn.metrics import r2_score
sklearn.metrics.r2_score(y_true, y_pred)

2. Adjusted R-Squared

Every additional independent variable added to a model always increases the R² value — therefore, a model with several independent variables may seem to be a better fit even if it isn’t. This is where Adjusted R² comes in. The adjusted R² compensates for each additional independent variable and only increases if each given variable improves the model above what is possible by probability.

There are a couple of ways to find the adjusted R² with Python:

Option 1: Manual Calculation

# n = number of sample size
# p = number of independent variables Adj_r2 = 1-(1-R2)*(n-1)/(n-p-1)
Option 2: statsmodel.api

import statsmodels.api as sm
from statsmodels.sandbox.regression.predstd import wls_prediction_std model1=sm.OLS(y_train,x_train)
result=model1.fit()
print(result.summary())

3. Mean Absolute Error (MAE)

The absolute error is the difference between the predicted values and the actual values. Thus, the mean absolute error is the average of the absolute error.

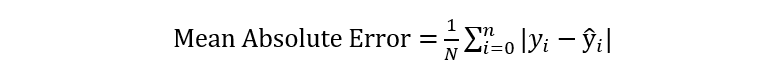
By importing mean_absolute_error from sklearn.metrics, you can compute easily compute the MAE of your model.

from sklearn.metrics import mean_absolute_error
mean_absolute_error(y_true, y_pred)

4. Mean Squared Error (MSE)

The mean squared error or MSE is similar to the MAE, except you take the average of the squared differences between the predicted values and the actual values.

Because the differences are squared, larger errors are weighted more highly, and so this should be used over the MAE when you want to minimize large errors. Below is the equation for MSE, as well as the code.

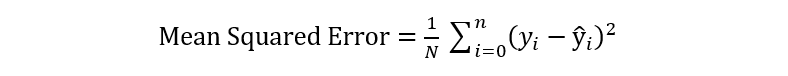
from sklearn.metrics import mean_squared_error

mean_squared_error(y_true, y_pred)

Infographic

MLOps Maturity Model [M3]

In this Infographic, you’ll learn:

The FIVE stages of maturity in Machine Learning Operations, i.e., MLOps
Why DevOps is not the same for ML as it is for software, and why MLOps is needed
The ideal teams, stacks, and features to look for to reach Maturity in your ML program

Learn why some companies succeed, while others struggle in AI/ML by seeing the signatures of success across Ideation, Team, Stack, Process, & Outcome in this informative (Hi-res) Infographic.

Infographic: MLOps Maturity Model [M3]

B) Evaluating Classification Models

5. Confusion Matrix and related metrics

A confusion matrix, also known as an error matrix, is a performance measurement for assessing classification models. Below is an example of a two-class confusion matrix.

Within the confusion matrix, there are some terms that you need to know, which can then be used to calculate various metrics:

True Positive: Outcome where the model correctly predicts the positive class.
True Negative: Outcome where the model correctly predicts the negative class.
False Positive (Type 1 Error): Outcome where the model incorrectly predicts the positive class.
False Negative (Type 2 Error): Outcome where the model incorrectly predicts the negative class.

Now that you know these terms, here are a number of metrics that you can calculate:

Accuracy: equal to the fraction of predictions that a model got right.

Recall: attempts to answer “What proportion of actual positives was identified correctly?”

Precision: attempts to answer “What proportion of positive identifications was actually correct?”

To really hit it home, the diagram below is a great way to remember the difference between precision and recall (it certainly helped me)!

Taken from Wikipedia
Code for confusion matrix and related metrics are below:

# Confusion Matrix
from sklearn.metrics import confusion_matrix
confusion_matrix(y_true, y_pred) # Accuracy
from sklearn.metrics import accuracy_score
accuracy_score(y_true, y_pred) # Recall
from sklearn.metrics import recall_score
recall_score(y_true, y_pred, average=None) # Precision
from sklearn.metrics import precision_score
precision_score(y_true, y_pred, average=None)

Formula for F1 Score
The F1 score is a measure of a test’s accuracy — it is the harmonic mean of precision and recall. It can have a maximum score of 1 (perfect precision and recall) and a minimum of 0. Overall, it is a measure of the preciseness and robustness of your model.

There are three ways you can calculate the F1 score in Python:

# Method 1: sklearn
from sklearn.metrics import f1_score
f1_score(y_true, y_pred, average=None)# Method 2: Manual Calculation
F1 = 2 * (precision * recall) / (precision + recall) # Method 3: BONUS – classification report
from sklearn.metrics import classification_report
print(classification_report(y_true, y_pred, target_names=target_names))

7. AUC-ROC Curve

The AUC-ROC Curve is a performance measurement for classification problems that tells us how much a model is capable of distinguishing between classes. A higher AUC means that a model is more accurate.

If you want to learn more about it, Sarang does a great job explaining it here.

To calculate the AUC-ROC score, you can replicate the code below:

import numpy as np
from sklearn.metrics import roc_auc_score y_true = np.array([0, 0, 1, 1])
y_scores = np.array([0.1, 0.4, 0.35, 0.8])
roc_auc_score(y_true, y_scores)
0.75
And that’s it! Now you know how to evaluate your machine learning models to determine if they’re actually useful. Next, we’ll go over various ways to improve your machine learning model.

For more articles like this one, check out https://blog.datatron.com/

Thanks for Reading!

Here at Datatron, we offer a platform to govern and manage all of your Machine Learning, Artificial Intelligence, and Data Science Models in Production. Additionally, we help you automate, optimize, and accelerate your ML models to ensure they are running smoothly and efficiently in production — To learn more about our services be sure to Book a Demo.